Trigonometry | Wolfram Resource Object

Trig Functions and Naming Conventions

Trig Functions: Everything Starts with Sine	Naming Conventions and Combining Operators
Applying Operators: Building New Functions	Other Functions Built from Sine

Trigonometric functions are functions that describe relationships between quantities in conics such as circles and hyperbolas.

Trig Functions: Everything Starts with Sine

There are a large number of "common" circular trig functions, each of which has a hyperbolic analogue. However, the vast majority of such functions can be built from only the sine function.

Sin [z]	the sine function (with argument in radians)
ArcSin [z]	the inverse of Sin [z]

All commonly-encountered circular trig functions can be built from the sine function.

The remaining commonly-encountered trig functions as well as an enormous collection of lesser-known ones can be built from sine by either applying operator(s) to the function (see below), forming quotients therefrom, or performing other miscellaneous operations thereto (also discussed below).

Applying Operators: Building New Functions

To derive the remaining "common" circular trig functions as well as the many lesser-known ones included in the Trigonometry paclet, there are several operators that can be applied to a given function. These operators will be clearly examined the sections that follow and should be understood in order to better understand the functions and naming conventions utilized in this paclet.

cof(x)

For a given function

f(x)

, denote by

cof(x)

the co-

f(x)

function defined by

cof(x)=f(π/2-x)

The most basic of these functions is the well-known cosine function, which is defined to be the co- version of the aforementioned

Sin

function.

Cos [z]	the cosine function (with argument in radians), cos(z)=sin(π/2-z)
ArcCos [z]	the inverse of Cos [z]

Cosine is just the "co" operator applied to sine.

With sine and cosine defined, two "new" functions can be defined by taking quotients.

Tan [z]	the tangent function, sin(z)/cos(z)
Sec [z]	the secant function, 1/cos(z)
ArcTan [z]	the inverse of Tan [z]
ArcSec [z]	the inverse of Sec [z]

"New" trig functions defined by taking quotients of sines and cosines.

From here, the co- operator can be applied to derive the commonly-used cosecant and cotangent functions.

Csc [z]	the cosecant function, csc(x)=sec(π/2-x)
Cot [z]	the cotangent function, cot(x)=tan(π/2-x)
ArcCsc[z]	the inverse of Csc [z]
ArcCot [z]	the inverse of Cot [z]

Applying the co- operator to get the rest of the commonly-used trigonometric functions.

The real power of the co- operator becomes more evident below, where co- is combined with other operators to produce an almost-limitless array of new trig functions.

verf(x)

For a given function

f(x)

, denote by

verf(x)

the versed

f(x)

, defined by

verf(x)=

2[f(x/2)]

The two most basic such functions are the versed sine and versed cosine, both of which are defined in the Trigonometry paclet.

Versine [z]	the versed sine function, versine(z)=2 2 sin (z/2)
Vercosine [z]	the versed cosine function, vercosine(z)=2 2 cos (z/2)
InverseVersine [z]	the inverse of Versine [z]
InverseVercosine [z]	the inverse of Vercosine [z]

Versed sine and versed cosine.

The shorthand formulas

versine(z)=1-cos(z)

and

vercosine(z)=1+cos(z)

are often employed; the equivalence of these expressions to the ones given in terms of

sin

and

cos

above can be easily verified using

FullSimplify

As mentioned above, there are many additional functions that can be built by combining the co- and ver- operators. For example, these two operators combine to produce

Coversine

and

Covercosine

, which are the co- versions of the

Versine

and

Vercosine

functions discussed above (i.e.,

coversine(z)=1-cos(π/2-z)=1-sin(z)

and

covercosine(z)=1+cos(π/2-z)=1+sin(z)

Coversine [z]	the coversed sine function, coversine(z)=1-cos(π/2-z)
Covercosine [z]	the coversed cosine function, covercosine(z)=1+cos(π/2-z)
InverseCoversine [z]	the inverse of Coversine [z]
InverseCovercosine [z]	the inverse of Covercosine [z]

Combining co- and ver- to get new lesser-known trig functions.

haf(x)

For a given function

f(x)

, denote by

haf(x)

the halved

f(x)

or haversed

f(x)

, defined by

haf(x)=f(x)/2

The most elementary of these comes as a combination of the ha- and ver- operators, producing the haversed sine and haversed cosine functions

Haversine

and

Havercosine

. Note that

Haversine

is an example of a lesser-known trig function included in the Wolfram Language while

Havercosine

is included only in this paclet.

Haversine [z]	the haversed sine function, haversine(z)=versine(z)/2= 2 sin (z/2)
Havercosine [z]	the haversed cosine function, havercosine(z)=vercosine(z)/2= 2 cos (z/2)
InverseHaversine [z]	the inverse of Haversine [z]
InverseHavercosine [z]	the inverse of Havercosine [z]

Haversed sine and haversed cosine are generated by combining the ha- and ver- operators.

As mentioned above, there are many additional functions that can be built by combining ha- with the co- and ver- operators. These come standard in the Trigonometry paclet.

Cohaversine [z]	the cohaversed sine function, cohaversine(z)=haversine(π/2-z)=1/2(1-sin(z))
Hacoversine [z]	the haversed coversine function, which is equivalent to Cohaversine [z] for all z
Cohavercosine [z]	the cohaversed cosine function, cohavercosine(z)=havercosine(π/2-z)=1/2(sin(z)+1)
Hacovercosine [z]	the haversed covercosine function, which is equivalent to Cohavercosine [z] for all z
InverseCohaversine [z]	the inverse of Cohaversine [z]
InverseHacoversine [z]	the inverse of Hacoversine [z] , also equivalent to InverseCohaversine [z]
InverseCohavercosine [z]	the inverse of Cohavercosine [z]
InverseHacovercosine [z]	the inverse of Hacovercosine [z] , also equivalent to InverseCohavercosine [z]

Lots of new functions can be built by combining co-, ver-, and ha-.

exf(x)

For a given function

f(x)

, denote by

exf(x)

the exterior, external, or outward

f(x)

, defined by

exf(x)=f(x)-1

The two most basic such functions are the exterior secant and exterior cosecant, both of which are defined in the Trigonometry paclet.

Exsecant [z]	the exterior secant function, exsecant(z)=sec(z)-1
Excosecant [z]	the exterior cosecant function, excosecant(z)=csc(z)-1
InverseExsecant [z]	the inverse of Exsecant [z]
InverseExcosecant [z]	the inverse of Excosecant [z]

Exsecant and excosecant.

Naming Conventions and Combining Operators

As demonstrated above, operators such as co-, ver-, ha-, and ex- can be combined to create new functions. For example, the result of the process

→ co- (yielding

) → ver- (yielding

) → ha- (yielding

) → co-

is the

Cohavercosine

function, provided in this paclet. This immediately raises some noteworthy questions.

One potential question is: Can we continue to apply more operators to create increasingly complex functions? The short answer is "Kind of..." in the sense that yes, you're more than welcome to do such a thing, but the end result may lack utility and hence be rendered pointless.

On the topic of utility, one may then ask: What about the functions in this paclet make them more useful than a function created by applying combinations of the four operators at random? Generally speaking, the inclusion of the functions in this paclet isn't meant to be a testament to how useful they are or aren't, but is instead meant highlight a subset of functions which gained some degree of use in the past. The fact is that

, and

(for example) have a historical footprint wherein authors from antiquity found them useful; thus, they were chosen for inclusion in this paclet.

Another worthwhile question stems from the observation that

Cohavercosine

is the exact same as the function

Hacovercosine

, which you get when you do

→ co- (yielding

) → ver- (yielding

) → co- (yielding

) → ha- (yielding

In particular, two very different processes involving two instances of co- plus one instance of ver- plus one instance of ha- both seem to yield the same function, even though the operators were applied in a different order. Is this typical? Does it matter in which order the operators applied when creating new functions?

Well, it depends. Some operators do "commute" (that is, yield the same result regardless of which order they're applied) while some do not. For example, ha-co-sine would be

1/2sin(π/2-z)

and so too would co-ha-sine. Conversely, ex-ver-sine would be

sin

(z/2)+1

while ver-ex-sine would be

(sin(z/2)+1)

, which is a different function altogether:

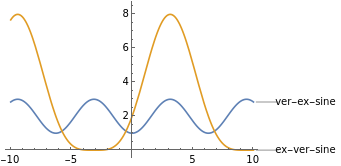
So, to summarize: Order sometimes matters, and in general, one should expect that applying a series of operators will result in a totally new function depending on which order is chosen.

Other Functions Built from Sine

The Trigonometry paclet also contains functions built from

Sin

which don't come from the four operators above.

Chord [z]	the chord function, chord(z)=2sin(z/2)
InverseChord [z]	the inverse of Chord [z]

In addition, the chord function satisfies a number of Pythagorean-like identities and could ostensibly be used in conjunction with the four operators above to derive other possibly-useful functions as well.